1.5 Χρωματικός κώδικας αντιστάσεων
Ο κώδικας χρωμάτων είναι ένας τρόπος που χρησιμοποιείται για να προσδιορίσουμε την ονομαστική τιμή της αντίστασης και της ανοχής σ’ ένα αντιστάτη.
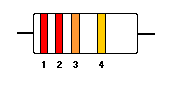
Η αντίσταση φέρει λεπτά έγχρωμα δαχτυλίδια όπως βλέπουμε στην παρακάτω εικόνα

Σε μία αντίσταση με τέσσερις χρωματικές λωρίδες ( όπως ο παραπάνω αντιστάτης ), οι τρεις πρώτες λωρίδες βρίσκονται σχετικά κοντά η μία στην άλλη και καθορίζουν την τιμή της αντίστασης, ενώ η τέταρτη που βρίσκεται λίγο μακρύτερα από τις υπόλοιπες τρεις υποδηλώνει την ανοχή της τιμής της αντίστασης. Το χρώμα της λωρίδας της ανοχής είναι συνήθως χρυσαφί ή ασημί. Αν δεν υπάρχει τέταρτη λωρίδα η ανοχή του αντιστάτη θεωρείται ίση με 20%.
Για να βρούμε την τιμή μίας αντίστασης, τοποθετούμε την αντίσταση έτσι ώστε η λωρίδα της ανοχής να βρίσκεται τελευταία ( δηλαδή δεξιά ). Τότε το πρώτο και το δεύτερο χρώμα ( πρώτη- δεύτερη λωρίδα ) αντιστοιχούν στα δύο πρώτα ακέραια ψηφία της αντίστασης. Το χρώμα της τρίτης λωρίδας είναι πολλαπλασιαστής και αντιστοιχεί στο παράγοντα ( δύναμη του 10 ) με τον όποιο πρέπει να πολλαπλασιαστούν τα ψηφία των δύο πρώτων λωρίδων. Ο αριθμός που προκύπτει είναι η τιμή της αντίστασης, ενώ βλέποντας την τέταρτη και τελευταία λωρίδα σημειώνουμε και την ανοχή της.
Παρακάτω βλέπουμε τον χρωματικό κώδικα αντιστάσεων.

Με τον χρωματικό κώδικα έχουμε μια πρώτη εκτίμηση ( προσέγγιση ) για την ονομαστική τιμή μίας αντίστασης. Η απευθείας μέτρησή της γίνεται με ειδικά όργανα τα πολύμετρα ( στην λειτουργία ‘’ ωμομέτρο’’ ).
Παράδειγμα
Στην επιφάνια μίας αντίστασης είναι τυπωμένες τέσσερις λωρίδες με χρώματα ( από αριστερά προς τα δεξιά ) : κίτρινο, μωβ , κόκκινο και χρυσαφί.
Η ονομαστική τιμή της αντίστασης θα είναι :
4 (κίτρινο) 7 (μωβ) 00 (κόκκινο) = 4700Ω = 4,7ΚΩ με ανοχή 5% (χρυσαφί).

Πραγματική μορφή αντίστασης.

Άσκηση 1
Παρατηρώντας τα χρώματα στις αντιστάσεις και με την βοήθεια του πίνακα χρωματικού κώδικα αντιστάσεων βρείτε την ονομαστική τιμή της αντίστασης.
 |  |  |  |
Αποτέλεσμα: (100Ω @ 5%) | Αποτέλεσμα: (22ΚΩ @ 5%) | Αποτέλεσμα: (2.2ΚΩ @ 5%) | Αποτέλεσμα: (2.7ΚΩ @ 5%) |
 |  |  |  |
Αποτέλεσμα: (47ΚΩ @ 2%) | Αποτέλεσμα: (470ΚΩ @ 5%) | Αποτέλεσμα: (560Ω @ 5%) | Αποτέλεσμα: (5.6ΚΩ @ 5%) |
 |  |  |  |
Αποτέλεσμα: (330ΚΩ @ 5%) | Αποτέλεσμα: (10ΜΩ @ 5%) | Αποτέλεσμα: (39ΜΩ @ 5%) | Αποτέλεσμα: (1ΜΩ @ 5%) |
ΑΣΚΗΣΗ 2
Να βρείτε την τιμή (σε ωμ) αντιστάσεων τον όποιον οι τέσσερις λωρίδες είναι:
Καφέ, μαύρο, καφέ, ασημί
Καφέ, μαύρο, πορτοκαλί, ασημί
Καφέ, κόκκινο, κόκκινο, χρυσαφί
Κίτρινο, μωβ, καφέ, ασημί
Πορτοκαλί, γκρι, καφέ, χρυσαφί
Μπλε, πράσινο, κόκκινο, κόκκινο
Άσκηση 3
Λύστε το σταυρόλεξο
Άσκηση 4
Κάντε την αντιστοίχιση
1.4 Εξάρτηση της αντίστασης από την θερμοκρασία
Είναι γνωστό ότι η αντίσταση ενός αγωγού εξαρτάται από τα γεωμετρικά του στοιχεία και δίνεται από την σχέση R= ρL/S όπου L είναι το μήκος του αγωγού, S η επιφάνεια της διατομής του και ρ ειδική αντίσταση που εξαρτάται από τη φύση του υλικού και της θερμοκρασίας.
Η σχέση που συνδέει την αντίσταση ενός αγωγού με τη θερμοκρασία έχει τη μορφή :
R=R0[1+α(θ-θ0)] σε [Ω]
Η αντίσταση του υλικού μεταβάλλεται με την θερμοκρασία.
Το R0 είναι η αντίσταση ενός αγωγού σε θερμοκρασία θ0.
Το α ονομάζεται θερμικός συντελεστής αντίστασης και εξαρτάται από το υλικό και έχει διάσταση 1/0C = grad-1. Συνηθίζεται να παίρνουμε τις μέσες τιμές του α για θερμοκρασία μεταξύ 0ο και 100ο C. Με καλή προσέγγιση θεωρούμε για τον συντελεστή α την θερμοκρασία των 20ο C.
Προσομοίωση
Παράδειγμα
Να υπολογισθεί η αντίσταση αγωγού χαλκού μήκους 200m και διατομής 4mm^2
ΛΥΣΗ
Συνηθίζεται για τους χάλκινους αγωγούς να λαμβάνεται στις εφαρμογές ως τιμή της ειδικής αντίστασης ρ=0,018
Από την σχέση R=ρ*l/s αντικαθιστώντας έχουμε:
R=0,018*(200m/4)=0.9Ω
1.3. Αντίσταση και Αγωγιμότητα
- το μήκος του αγωγού (σύρμα) (Ι)
- τη διατομή του σύρματος (s)
- Την χημική σύσταση του υλικού του σύρματος (ρ)
Ο συντελεστής ρ ονομάζεται ειδική αντίσταση.
Η ειδική αντίσταση μετριέται σε Ωmm^2/m, η διατομή S σε mm^2, η αντίσταση R σε Ω και το μήκος 1 σε m.
Η σχέση επιλύεται ως προς Ι και S και προκύπτουν:
Ι=RS/ρ[m]
S=ρl/R [mm^2]
Από τις παραπάνω σχέσεις υπολογίζονται το μήκος του αγωγού από το οποίο κατασκευάζεται μια ωμική αντίσταση και η διατομή του.
1.3.1 Αγωγιμότητα.
Η αγωγιμότητα εκφράζει την ευκολία της μετακίνησης των ηλεκτρονικών φορτίοων μέσα στον αγωγό. Υψηλές τιμές αγωγιμότητας σημαίνει μεγάλη ευκολία στην κίνηση του ηλεκτρικού φορτίου.
Η ηλεκτρική αντίσταση R ειναι το αντίστροφο της αγωγιμότητας.
R= 1/ G επομένως G=1/R
Όπου G ειναι η αγωγιμότητα σε omh, ή Siemens (s).
1.3.2 Ειδική Αγωγιμότητα.
Η ειδική αντίσταση είναι το αντίστροφο της ειδικής αγωγιμότητας.
ρ= 1/ κ επομένως κ=1/ρ
όπου κ είναι η ειδική αγωγιμότητα σε [ m/ Ωmm^2 ]
Η ειδική αντίσταση και η ειδική αγωγιμότητα (στους 20 βαθμόυς C ) διαφόρων αγώγιμων υλικών βρίσκεται στον παρακάτω πίνακα.

Προσομοίωση
Επεξήγηση προσομοίωσης
1.2. Ο Νόμος του Ωμ σε πλήρες κύκλωμα
Ηλεκτρεγερτική δύναμη είναι η τάση μεταξύ των πόλων της πηγής, όταν από την πηγή δεν διέρχεται ηλεκτρικό ρεύμα (ανοιχτό κύκλωμα).
Η εσωτερική αντίσταση της πηγής εκφράζει την δυσκολία που συναντούν τα ηλεκτρικά φορτία κατά την κίνηση τους στο εσωτερικό της πηγής.
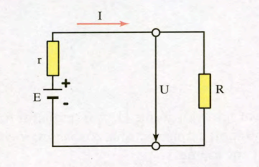
Σχήμα 1.3. Πλήρες κλειστό κύκλωμα με πηγή και εξωτερική ωμική αντίσταση

Σχήμα 1.3.α. ανοιχτοκυκλωμένο κύκλωμα (ανοιχτό)

Σχήμα 1.3.β. Βραχυκυκλωμένο κύκλωμα (βραχυκύκλωμα)
Ο νόμος του Ohm σε πλήρες κύκλωμα εκφράζεται από την σχέση :

Ισχύει ότι :
Ε=IR+Ir=U+Ir και από αυτή U=E-Ir
Όπου: Το γινόμενο IR είναι η πτώση τάσης U, που μετριέται στα άκρα της αντίστασης R.
Παράδειγμα
Η εσωτερική αντίσταση πηγής είναι 1Ω και η πολική της τάση 60V. Η ωμική αντίσταση που είναι συνδεδεμένω στα άκρα της διαρρέεται από ρεύμα έντασης 5Α. Να βρεθεί η ΗΕΔ της πηγής.
Λύση
Η ΗΕΔ της πηγής βρίσκεται από τον νόμο του Ωμ σε πλήρες κύκλωμα:
Ε=U+I*r=60V+5A*1Ω=65V
Προσομοίωση
1.1. Νόμος του Ωμ

Σχήμα 1.2. Σύνδεση πέντε μπαταριών σε σειρά, με αμπερόμετρο και ηλεκτρική αντίσταση.
Με βάση το σχ.1.2 αποδεικνύεται ότι R=V/I

Αυτό σημαίνει ότι η σχέση τάσης και ρεύματος για μια ηλεκτρική αντίσταση είναι "γραμμική".
Η κλίση της ευθείας γραμμής αντιστοιχεί με την τιμή της αντίστασης που χρησιμοποιήσαμε.
Παράδειγμα
Στους ακροδέκτες Α και Β της αντίστασης R, που διαρρέεται από ρεύμα I=10A, επικρατεί τάση ίση με U=220V. Να βρεθεί η τιμή της ωμικής αντίστασης.
Λύση
Εφαρμόζοντας τον νόμο του Ohm βρίσκουμε: R=U/I=220V/10A=22Ω
Προσομοίωση
Επεξήγηση προσομοίωσης
Βασικές Έννοιες Φυσικής
Το ηλεκτρικό φορτίο είναι ένα θεμελιώδες μέγεθος του ηλεκτρισμού. Όταν τα ηλεκτρικά φορτία κινούνται ή ηρεμούν, τότε ασκούν δυνάμεις σε άλλα ηλεκτρικά φορτία που κινούνται ή είναι ακίνητα. Οι δυνάμεις αυτές είναι οι ηλεκτρομαγνητικές δυνάμεις.
Η ποσότητα ηλεκτρικού φορτίου του ενός ηλεκτρονίου είναι ίση με 1,6* 10^(-19) Coulomb και είναι η μικρότερη γνωστή. Η φορά της κίνησης των ηλεκτρονίων είναι από το τμήμα όπου υπάρχει συσσώρευση ηλεκτρονίων προς το τμήμα όπου υπάρχει έλλειψη.
Μονάδα μέτρηςη του ηλεκτρικού φορτίου είναι το 1 Coulomb στο Διεθνές Σύστημα S.I. Το Coulomb ορίζεται σαν το φορτίο 6,24*10^18 ηλεκτρονίων και είναι το φορτίο που μεταφέρεται σε 1" από ηλεκτρικό ρεύμα 1 Αmpere.
1Cb=1A*1sec
Συνεχές ρεύμα είναι το ρεύμα του οποίου η τιμή παραμένει σταθερή σε κάθε χρονική στιγμή t. (σχ.1)

Η ηλεκτρική τάση μεταξύ δυο σημείων είναι το έργο που απαιτείται για την μετακίνηση μιας μονάδας θετικού ηλεκτρικού φορτίου από το ένα σημείο στο άλλο.
